Das Virus und die Mathematik

Zugegeben: In Mathe war ich nicht wirklich gut. Aber was ich auf diesem Gebiet gelernt habe, auf der Schule und im Studium, reicht immerhin, um einigen Fehlschlüssen im Zusammenhang mit der Corona-Pandemie zu entgehen.

Ein Virus hat nicht viel vom Leben – es lebt ja nicht einmal richtig, denn es hat weder einen Stoffwechsel, noch kann es sich aus eigener Kraft vermehren. Es ist auch nicht eigentlich bösartig, denn wenn es seinen Wirt umbringt, ist das nur eine Nebenwirkung. Ein Virus ist ein gekapselter und damit vor Umwelteinflüssen geschützter Programmcode, der die Zellen eines Wirtsorganismus so umprogrammiert, dass sie sich der Produktion weiterer Viren der gleichen Art widmen.

Wenn das Immunsystem des Wirts mit dem Virus fertig wird, ist das sein Ende; wenn es versagt und der Wirt stirbt, ist es das ebenfalls. Ein erfolgreiches Virus muss, nachdem es einen Wirt gefunden hat, mehr als einen weiteren geeigneten Wirtsorganismus infizieren. Liegt die Infektionsquote unter 1,0, dann bricht die Seuche zusammen und das Virus verschwindet, aber je höher sie über 1,0 liegt, desto rasanter breitet sich die Seuche aus. Man spricht dann von einer Epidemie oder, wenn sich das Virus über mehrere Erdteile ausbreitet, von einer Pandemie.

Die Ausbreitung des Virus folgt zunächst einer Exponentialfunktion. Was eine exponentielle Steigerung bedeutet, kennen wir von der Legende über den Erfinder des Schachspiels, der sich als Lohn ein Reiskorn auf dem ersten Feld des Schachbretts wünschte, zwei auf dem zweiten, vier auf dem dritten, also jeweils die doppelte Zahl von Reiskörnern des vorigen Feldes. Das fängt harmlos an, aber auf dem letzten der 64 Felder müssten 9,2233720369 × 10¹⁸ Körner liegen, eine unvorstellbar große Zahl. Die exponentielle Verbreitung der Infektionen endet, wenn es immer mehr Infizierte gibt und das Virus daher immer mehr Probleme hat, noch einen gesunden und nicht bereits immunen Wirtsorganismus zu finden. Irgendwann erreichen wir eine sogenannte Herdenimmunität, weil das Virus nicht mehr zu den wenigen noch verbliebenen möglichen Opfern durchdringen kann. Die Alternative besteht darin, die Ansteckungsrate zu verringern, indem Kontakte zwischen Menschen, bei denen das Virus überspringen kann, verringert werden. Falls die Ansteckungsrate unter 1,0 sinkt, stirbt das Virus aus; wird sie zumindest kleiner, bleibt die Ausbreitung zwar exponentiell, wird aber gebremst – man gewinnt damit Zeit, um beispielsweise einen Impfstoff zu entwickeln.

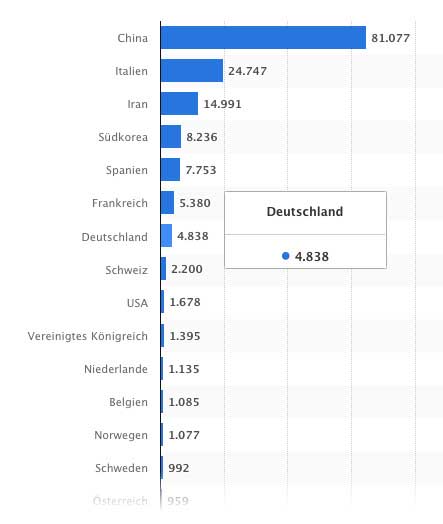
Der erste verbreitete Fehlschluss entsteht dadurch, dass wir uns nicht den exponentiellen Charakter der Ausbreitung vergegenwärtigen. Wir vergleichen beispielsweise die Zahl der Infizierten in Deutschland mit den Zahlen aus China, dem Iran oder Italien, stellen fest, dass die Lage bei uns lange nicht so dramatisch aussieht wie in jenen Ländern, und wiegen uns daher in Sicherheit. Bei einer exponentiellen Steigerung bedeutet eine geringere Zahl der Infizierten jedoch nur, dass die Ausbreitung der Epidemie bei uns später begonnen hat. Der Faktor, also die Zahl derjenigen, die jeder Virenwirt im Durchschnitt ansteckt, ist bei uns derselbe. Wir befinden uns zwar noch an einem früheren Punkt der Kurve, werden aber Tage oder Wochen später ähnlich hohe Zahlen verzeichnen, wenn wir nichts gegen die Verbreitung des Virus tun.

Ein anderer Fehlschluss unterläuft uns, wenn wir die Sterblichkeitsquote berechnen wollen. In China sind (nach den von statista erhobenen Daten) 81077 Menschen als infiziert bekannt; dem stehen 3218 Todesfälle durch COVID-19 gegenüber. Das entspräche einer Quote von 3218 / 81077 = 4,0 Prozent. In Deutschland sind es 4838 bekannte Infektionen und 12 Todesfälle, was lediglich 0,25 Prozent entspricht. Ist die Überlebenswahrscheinlichkeit in Deutschland also vielfach höher als in China – vielleicht weil unser Gesundheitssystem besser wäre? Leider ist dem nicht so – die Überlebenswahrscheinlichkeit kann höher oder niedriger als die in China sein, aber aus diesen Zahlen können wir das nicht ersehen.

Wie viele Menschen an COVID-19 gestorben sind, wissen wir relativ genau (obwohl es Zweifelsfälle gibt, wenn jemand erst nach dem Tod positiv getestet wird und man zunächst nicht sicher weiß, ob das Virus die Todesursache war). Problematischer ist die Bestimmung der Bezugsgröße. Wir können nicht mit der aktuell bekannten Zahl von Infektionen rechnen, denn die entscheidende Zahl ist die der Infektionen zu dem Zeitpunkt, als sich der letzte Tote angesteckt hatte. Ein typischer tödlicher Verlauf von COVID-19 dauert 14 Tage, so dass wir die Zahl der Infektionen vor 14 Tagen bräuchten. Diese kennen wir jedoch nicht, denn wir wissen ja nur, wie viele Infektionen vor 14 Tagen bekannt waren, weil entsprechende positive Testergebnisse vorlagen. COVID-19 hat aber eine Inkubationszeit von mindestens fünf Tagen; erst fünf Tage nach der Infektion treten die ersten Symptome auf und erst dann wird der Betroffene vielleicht darüber nachdenken, sich testen zu lassen. Bis der Test erfolgt ist und das Ergebnis vorliegt, vergehen weitere Tage, und die Tage von der Ansteckung bis zum positiven Testergebnis müssen wir von den angenommenen 14 Tagen abziehen. Das ergibt dann eine knappe Woche. Allerdings lassen sich manche testen, die zwar noch symptomfrei sind, aber aus einem Risikogebiet kommen oder Kontakt zu einem bekannten Infizierten hatten, und dann kann das Testergebnis früher vorliegen. In jedem Fall müssen wir mit der Zahl der Infizierten zu einem früheren Zeitpunkt rechnen, und da diese geringer – aufgrund der Exponentialfunktion oft viel geringer – als die aktuelle Zahl ist, liegt die Sterblichkeitsquote höher, als wir naiverweise annehmen. Der aus den chinesischen Zahlen ermittelte Wert dürfte realistisch sein, weil sich der Anstieg der Infektionszahlen in China schon seit etwa drei Wochen abgeflacht hat und es daher keinen so großen Unterschied zwischen den Zahlen zu verschiedenen Zeitpunkten mehr gibt.

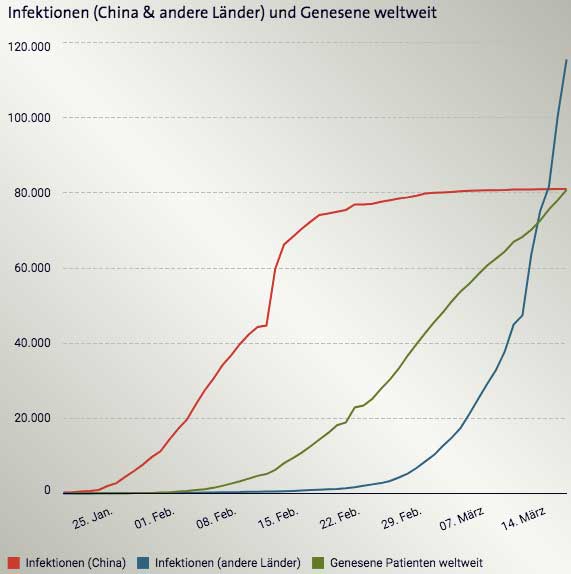
Als alternativer Rechenweg wird bisweilen empfohlen, die Zahl der Todesfälle durch die Summe der Todesfälle und der Zahl der Genesenen zu teilen, aber auch diese Rechnung ist mit Fehlern behaftet. Wie viele Infizierte genesen sind, ist nicht so genau (oder wird erst verzögert) bekannt, auch weil manche milde Krankheitsverläufe gar nicht als COVID-19 oder überhaupt als Erkrankung erkannt werden. Zudem dauert die Genesung typischerweise länger als ein tödlicher Verlauf, so dass die miteinander verrechneten Werte gar nicht vergleichbar sind.

Die exponentielle Verbreitung und die lange Inkubationszeit, also die Zeit von der Ansteckung bis zum Ausbruch der Krankheit, führt leider auch dazu, dass wir den möglichen Erfolg der Maßnahmen, die Epidemie einzudämmen, zunächst gar nicht erkennen können. Wenn es uns auf irgendeine Weise gelänge, die Zahl der Neuinfektionen von heute auf morgen auf Null zu drücken, wäre das der Statistik nicht anzusehen. Wer jetzt infiziert ist, erfahren wir ja meist erst nach der Inkubationszeit und den dann durchgeführten Tests. In der nächsten Woche würde die Zahl der bekannten Infizierten daher weiter exponentiell ansteigen, so als hätten die ergriffenen Abwehrmaßnahmen gar keine Wirkung. Die Zahl der Todesfälle würde sogar noch zwei Wochen lang weiter steigen. Obwohl wir also die Epidemie erfolgreich gestoppt hätten, würden die täglich aktualisierten Zahlen ein ganz anderes, irreführendes Bild zeichnen.

Das ist vermutlich einer der Gründe, weshalb die Politik die Maßnahmen im Tagesrhythmus eskaliert. Als ich vor einer Woche hier im Blog die Illustration zum Motto „Flatten the curve“ zeigte, ging es noch um ganz simple Vorsichtsmaßregeln, um das Virus nicht leichtfertig zu verbreiten – sich also regelmäßig die Hände zu waschen und in die Armbeuge zu niesen, statt virenbehaftete Körperflüssigkeit im weiten Umkreis zu verbreiten. Dann wurden große und schließlich auch kleinste Veranstaltungen verboten und heute ist nicht nur das gewohnte Freizeitleben, sondern auch die Erwerbstätigkeit vieler Menschen auf unabsehbare Zeit eingestellt. So lange keine Erfolge sichtbar werden – und das ist, wie gesagt, prinzipbedingt gar nicht vor zwei Wochen möglich –, traut sich kein Politiker, auf noch radikalere Eingriffe in unsere Freiheit zu verzichten. Ob das vielen Menschen das Leben rettet oder in so radikaler Form gar nicht nötig wäre, wissen wir nicht. Und daher wissen wir auch nicht, ob die nun drohende Insolvenzwelle vieler kleiner Betriebe und Freiberufler ein Risiko ist, das man eingehen muss.

Die allgemeine Unsicherheit bringt manche auf die Idee, es sollte endlich massenhafte Tests auf Infektionen mit dem SARS-CoV-2-Virus geben. Mal abgesehen davon, dass der nötige Aufwand immens wäre, bliebe die Aussagekraft solcher Tests begrenzt. Nehmen wir einmal an, der Test würde jeden Virenbefall zuverlässig erkennen – was er nicht wirklich tut, aber in diesem Zusammenhang können wir darüber hinweg sehen. Von 1000 Infizierten würden also 1000 erkannt. Unter 1000 getesteten Gesunden würden dagegen 999 das korrekte negative Resultat erhalten, einer aber ein fälschlich positives. Das wäre eine False-Positive-Rate von 0,001 und damit ein im Grunde sehr guter Wert – der Test geht nur in einem Promille der Fälle fehl. Nehmen wir weiter an, es gäbe in Deutschland aktuell 20000 Infizierte – vielleicht sind es noch mehr, aber es geht hier nur um eine Hausnummer. Bei 83 Millionen Deutschen wären also von 4150 Personen nur einer infiziert, 4149 aber gesund. Von den 4149 virusfreien Gesunden würden 4149/1000, also gut vier, fälschlicherweise ein positives Ergebnis erhalten. Zusammen mit dem einen Infizierten (den der Test, wie angenommen, korrekt erkennt) wären das fünf positive Ergebnisse, von denen vier, also 80 Prozent, falsch sind. Obwohl der Test in 999 von 1000 Fällen das richtige Ergebnis liefert, wären seine positiven Ergebnisse, entgegen der Intuition, meist falsch.

Solche irritierenden Ergebnisse, aufgrund derer sich das Gesundheitssystem verzettelte, weil es sich um Leute kümmern müsste, die in ihrer Mehrzahl tatsächlich gesund sind, gibt es immer, wenn die a-priori-Wahrscheinlichkeit für ein positives Testergebnis sehr gering ist. Es wäre anders, wenn ein großer Prozentsatz der Bevölkerung bereits infiziert wäre – aber das wollen wir ja eigentlich vermeiden. Die a-priori-Wahrscheinlichkeit wäre aber auch dann höher, wenn nur bei Vorliegen konkreter Verdachtsmomente getestet wird, also wenn entweder einschlägige Symptome vorliegen oder eine Infektion aus anderen Gründen wahrscheinlich ist – weil man sich in einem bekannten Risikogebiet aufgehalten oder Kontakt mit einem später Erkrankten hatte. Und so wird die Anwendung der Tests ja auch praktiziert.

Was aber folgt aus all dem? Was die nächsten Wochen bringen werden, kann uns weder die Mathematik noch die Virologie sagen, obwohl die Virologen, bisweilen unterschiedlicher Einschätzungen zum Trotz, einen großartigen Job machen, das Virus zu erforschen und die Ergebnisse mit den Kollegen zu teilen. Ich gehe aber beispielsweise nicht mehr davon aus, dass die photokina 2020 stattfinden wird, und plane daher keinen Besuch. Das Umweltfotofestival in Zingst behalte ich aber erst einmal weiter auf der Rechnung – schaun wir mal.