Rechnen wir es aus!
Kunst und Mathematik gehen ja für manche nicht zusammen, aber manchmal ist eine Formel der schnellste oder sogar der einzige Weg, ein Problem der Bildgestaltung zu lösen. Rechnen wir es aus!

Knifflige Leserfragen an die DOCMA-Redaktion beantwortet ja fast immer Doc Baumann, aber eine in der aktuellen Ausgabe DOCMA 98 beantwortete Frage war ausnahmsweise bei mir hängengeblieben. Dabei ging es um die Perspektive, also eines von Docs Lieblingsthemen, aber in diesem Fall war mit den klassischen Perspektivkonstruktionen mit zeichnerischen Mitteln wenig auszurichten – man musste rechnen.
Die Mathematik hat bekanntlich wenig Freunde, und niemand wird gering geschätzt, der zugibt, in Mathe nie besonders gut gewesen zu sein. Einerseits ist das beruhigend, aber andererseits ist es schade, dass die Mathematik so wenig wichtig genommen wird. Im täglichen Leben kann sie nämlich durchaus nützlich sein. Nicht unbedingt die Themen aus dem Leistungskurs – wer in der Schule mutmaßte, symbolisches Differenzieren und Integrieren, komplexe Zahlen oder Matrizenrechnung nie wieder zu benötigen, lag wahrscheinlich richtig. Umgekehrt war der Minderheit, die eine naturwissenschaftliche Ausbildung anstrebte, auch klar, dass sich die Mühe für sie immerhin lohnen würde.
Die im Alltag nützlichsten Anwendungen der Mathematik setzen durchweg nicht mehr als die Grundrechenarten voraus, und nachdem der Taschenrechner ja nun auch schon ein halbes Jahrhundert alt (und mittlerweile in das Smartphone integriert) ist, muss man nicht einmal gut und schnell rechnen können. Entscheidend ist es vielmehr, eine Problemstellung durch zahlenmäßig erfassbare Größen beschreiben zu können, so dass man sich einen gesuchten Wert einfach ausrechnen kann. Leider trägt der schulische Mathematikunterricht wenig dazu bei, dass man sich diese Fähigkeit aneignet.
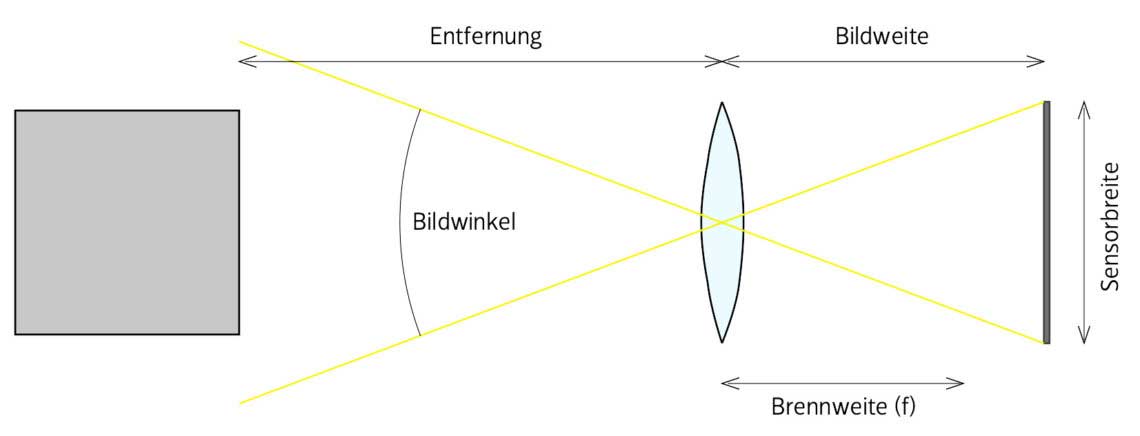
Die konkrete Leserfrage drehte sich darum, wie man eine perspektivische Zeichnung so anlegt, dass sie einem Foto mit einer vorgegebenen Brennweite entspricht. Ich habe diese Frage dann noch um ihr Gegenteil erweitert: Wie findet man die Brennweite, mit der sich die Perspektive eines gegebenen Fotos oder Gemäldes fotografisch nachstellen ließe? Und zur Beantwortung beider Fragen muss man rechnen.
Die benötigten Formeln sind simpel. Da gibt es einmal die Linsengleichung
1 / Entfernung + 1 / Bildweite = 1 / Brennweite
die die Bedingungen für ein scharfes Bild angibt; für eine näherungsweise Rechnung können Sie aber auch einfach Bildweite = Brennweite setzen. Dann gilt
Brennweite = Entfernung × Sensorbreite / Breite der erfassten Szene
und
Entfernung = Brennweite × Breite der erfassten Szene / Sensorbreite
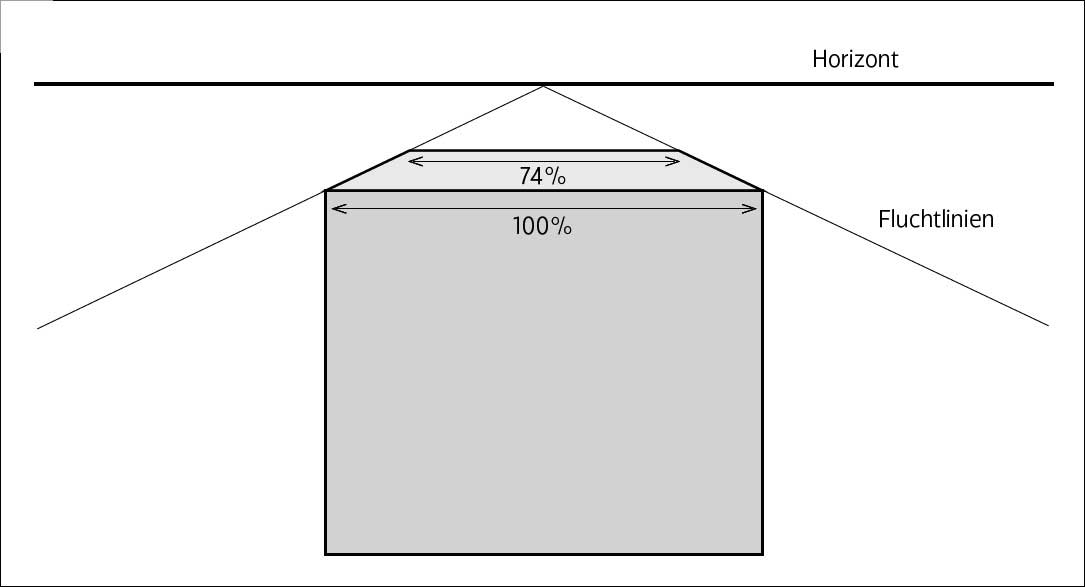
Die perspektivische Verkürzung bei einem Motiv mit bekannter Tiefe lässt sich mit
Verkürzung = Entfernung / (Entfernung + Tiefe)
berechnen, und mit diesem Ergebnis können Sie die ersten Fluchtlinien ziehen; die weitere Perspektivkonstruktion ergibt sich daraus:
Im Artikel beschreibe ich die Berechnung beispielhaft im Detail, und dort können Sie dann auch nachlesen, mit welcher Brennweite ein Bild wie Caravaggios Das Abendmahl in Emmaus nachzustellen wäre und wie man diese berechnet.











Ich habe eine leicht andere Frage: wie lautet die Formel, um den Öffnungs-WINKEL in Abhängigkeit von der Brennweite (bei gegebener Sensorgrösse) zu berechnen ?
Ciao Christoph
Die Formel lautet ω=2 ArcTan(f/(d/2), wobei ω der gesuchte Öffnungswinkel, f die Brennweite und d/2 der halbe Sensordurchmesser ist. Zustande kommt die Formel durch folgende geometrische Überlegungen …
Für ein Objekt im Unendlichen wird in der von M. Hussmann aufgeführten Formel 1/Entfernung = 0 und damit aus der verbleibenden Formel 1/Bildweite = 1/Brennweite nach etwas jonglieren die Bildweite zur Brennweite. Da sich der Öffnungswinkel auf die Bilddiagonale bezieht, entsteht nun zwischen Optik und Sensor ein imaginäres Dreieck aus der Kathete der optischen Achse durch die Optik- und Sensormitte, einem schrägen Strahl als Hypothenuse durch Optikmitte und Sensorecke und einer weiteren Kathete d/2 von der Sensormitte zur Sensorecke. Gemäss den trigonometrischen Bestimmungsgleichungen ist der Halbwinkel ω/2 gleich dem ArcusTangens aus den Quotient der beiden Katheten oder eben der Halbdiagonale d/2 geteillt durch die Bildweite (b) = Brenweite (f).
Die Rechnung zeigt, dass die Formel stimmt. Für einen Kleinformatsensor ist die halbe Sensordiagonale nach Pythagoras Wurzel(36^2+24^2)mm/2=21.6mm. Für mein Objektiv f=85mm wird der Öffnungswinkel nun zu 2ArcTan(21.6mm/85mm) = 28.5°, was für mein Nikon AF-S NIKKOR 85mm f/1.4G genau den technischen Daten entspricht. Eine Skizze bei der Geometrie ist zum Verständnis eventuell hilfreich, war aber hier leider nicht möglich.
Gruss, Peter
Ja, über den Arcustangens kommt man auf den Winkel. Man kann zwar statt der vereinfachend verwendeten Brennweite (mit der man den Winkel bei einer Fokussierung auf Unendlich erhält) auch die eigentlich korrekte Bildweite einsetzen, die bei kürzeren Entfernungen größer als die Brennweite ist, aber die Berechnung der Bildweite ist in der Praxis nicht so einfach. Die Linsengleichung weist den Weg, aber nur, wenn das Objektiv durch Auszugsverlängerung fokussiert.
Bei einer Innenfokussierung kann sich statt des Auszugs auch die Brennweite und/oder der bildseitige Nodalpunkt verschieben, und was da bei einem bestimmten Objektiv ganz genau passiert, ist durchweg nicht dokumentiert. Da kann man dann auch gleich mit der Brennweite rechnen und einen kleinen Fehler hinnehmen.