Bildkritik: Der Fluch der eingerollten Ecke
Immer wieder sieht man in der Werbung geknickte oder eingerollte Ecken eines Papierbogens, hinter denen sich dann das eine oder andere verbirgt. Und in den meisten Fällen sind diese Ecken per Photoshop erzeugt – und falsch. Die Bildbearbeiter haben offensichtlich etwas schräge Vorstellungen von Geometrie und Perspektive. Zusätzlich zeigt Ihnen Doc Baumann, wie Sie in Photoshop auch die Länge gekrümmter Linien messen können.

Heute geht’s mal nicht um den Enkeltrick, sondern um den Eckenknick. Schon vor vielen Jahren habe ich in DOCMA in meiner „Bildkritik“ eine ganze Sammlung falscher Eckenknicke vorgestellt. Gebessert hat sich seit damals dennoch nichts. Aktuell erneut aufgefallen ist mir dieser alte Fluch der falsch eingerollten Ecke, die eigentlich dafür sorgen soll, dass das Bild plastischer aussieht, als mir eine Abo-Werbung der Programmzeitschrift „TV-Spielfilm“ in die Hände fiel.

Das Hauptproblem ist immer dasselbe: Die Kanten der eingerollten oder umgeknickten Ecke können nie länger sein als die Strecke vom Beginn des Knicks bis zur Ecke des ursprünglichen Bogens. Bei einer einfachen Faltung um 180° sind sie exakt genau gleich lang, bei einer Einrollung oder wenn die Ecke nach oben steht, immer kürzer. In den Werbebeispielen jedoch sind diese Kanten oft deutlich länger als im Urspungszustand, und das kann nicht sein.

Weitere Fehler sind übertrieben abgerundete Kanten, und oft wird sogar die außen sichtbare Grenzlinie der Einrollung gebogen dargestellt, was ebenso unmöglich ist. Das zumindest ist bei unserem Beispiel nicht der Fall. Dafür gibt es unten einen unplausiblen Übergang zwischen einem harten Knick und einer sich dann noch oben fortsetzenden Rundung.
„Zurück-gerollt“ wären solche Ecken also immer größer als das ursprüngliche Papier und würden weit überstehen.
Gebogene Kanten nachmessen
Zwar sieht man, dass die untere Papierkante in unserem Werbebeispiel viel zu lang ist – aber wie misst man das nach? Photoshop bietet zwar verschiedene Messmethoden, aber die Länge eines Pfades ist so – anders als in Illustrator – nicht zu ermitteln.
Über einen kleinen Umweg lässt sich das dennoch realisieren: Folgen Sie zunächst der Papierkante mit dem Pfadwerkzeug. Legen Sie dann eine neue Werkzeugspitze an, die aus einem kleinen Quadrat festgelegter Größe besteht. Erzeugen Sie eine neue Ebene. Bei den Einstellungen des Pinsels wählen Sie bei »Formeigenschaften« für die Winkel-Steuerung »Richtung«, unter »Pinselform« stellen Sie den (Mal-) »Abstand« so ein, dass zwischen den Quadraten eine schmale Lücke bleibt.
Im »Pfade«-Bedienfeld klicken Sie, bei aktiviertem Pinsel, unten auf das Icon für »Pfadkontur mit Pinsel füllen«. Nun müssen Sie nur noch die Anzahl der Quadrate zählen und mit der Pixellänge der einzelnen Quadrat-Spitze multiplizieren. Dann haben Sie die Länge gemessen.
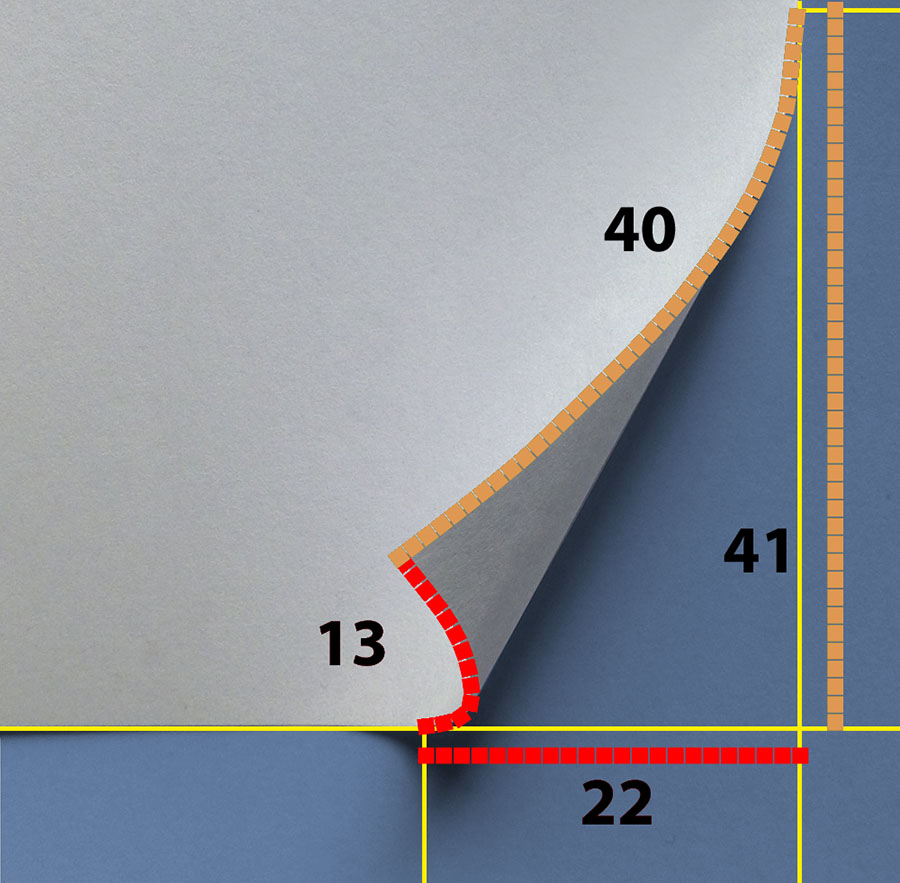

Da es in unserem Fall auf die absolute Länge nicht ankommt, habe ich nur die Quadrate ausgewählt. Beim fotografierten Knick ist die Länge von der ursprünglichen Papierecke zum Beginn des Knicks 22 Einheiten lang – eingerollt 13. Beim Werbebeispiel dagegen beträgt die Ursprungslänge 11 Einheiten, die der Rundung ist jedoch doppelt so groß, nämlich 22. Das führt dazu, dass die längere Kante nun nur noch 32 Einheiten lang ist statt der ursprünglichen 41, während sie beim fotografierten Papierbogen mit 40 Einheiten nur unwesentlich kürzer ist.
Einfacher Eckenknick
Eine ganz einfache Lösung, um auf der sicheren Seite zu sein, ist die Verwendung des ursprünglichen, rechteckigen Papierbogens.
1. Erzeugen Sie an der Ecke mit gedrückter Alt-Taste eine schräge Lasso-Auswahl, heben Sie den Auswahlbereich (grau) auf eine neue Ebene (Strg/Befehl-Alt-J-Tasten, also nicht nur duplizieren).

2. Spiegeln Sie das entstandene Dreieck horizontal und fügen Sie es durch Drehen und Verschieben genau an die Knickkante an. Jetzt liegen die beiden Papierflächen parallel zueinander, das Papier wäre also um 180° gefaltet.

3. Dunkeln Sie das Dreieck ab, transformieren Sie es, so dass die Ecke aufgerichtet erscheint, und legen Sie auf einer Ebene darunter einen zur Lichtrichtung passenden Schlagschatten an. Achten Sie beim Transformieren darauf, dass keine der Kanten länger wird als in ihrem Ausgangszustand.

4. Gegebenenfalls ergänzen Sie auf einer neuen Ebene eine dünne weiße Linie entlang der geknickten Papierkante und filtern sie mit »Störungen hinzufügen«.










Bildkritik an Bildkritik
Der einfache Eckenknick wirkt mit Schattenwurf und Abdunklung perfekt, ist jedoch in dieser Form in der Realität nicht möglich. Schön, aber falsch.
Der Beweis lässt sich mit den Regeln der Geometrie führen: Wenn ein rechtwinkliges Dreieck um die Hypotenuse rotiert, wird die Höhe über der Hypotenuse zum Radius einer Kreisfläche im Raum. Da diese rechtwinklig zur Hypotenuse liegt, erscheint die Kreisfläche in der Draufsicht als Gerade mit der Länge des Durchmessers. Zur Erinnerung: Die Höhe ist das Lot auf der Hypotenuse zur gegenüberliegenden Ecke.
Nun die Anwendung: Die abgeknickte Ecke hat die Form eines rechtwinkligen Dreiecks, bei dem die Knickkante die Hypotenuse ist. Den Knickvorgang kann man sich als Rotation um die Hypotenuse vorstellen. Damit beschreibt die Papierecke in der Draufsicht eine Gerade von der nicht geknickten bis zur voll umgeknickten Position. Beim einfachen Eckenknick muss die Ecke immer auf dieser Geraden liegen. Im konstruierten Bild liegt die Ecke aber darüber. Somit ist diese Darstellung in der Realität nicht möglich.
Ich hoffe, dass diese Erklärung verständlich ist. Das Kommentarfeld gestattet leider keine Grafik; bei Bedarf stelle ich diese gern auf anderem Weg zur Verfügung.
Ich möchte diesen Kommentar nicht ohne den Versuch einer Ehrenrettung für den Photoshop-Papst abschließen: Das Bild mit dem einfachen Eckenknick könnte doch korrekt sein. Der Betrachter müsste nur schräg auf das Papier schauen.
PS: Mit Hilfe der Geometrie könnte bei den gebogenen Ecken eine Fläche konstruiert werden, in der die Papierecken liegen müssen. Damit kann recht einfach überprüft werden, ob eine gebogene Ecke korrekt ist.